Land of Math

Finding the Area of Triangles

One of the struggles every year for some middle school students is finding the Area of Triangles. In this blog we will look at a few ways to help explain the process and make it a bit easier.

Key Terms

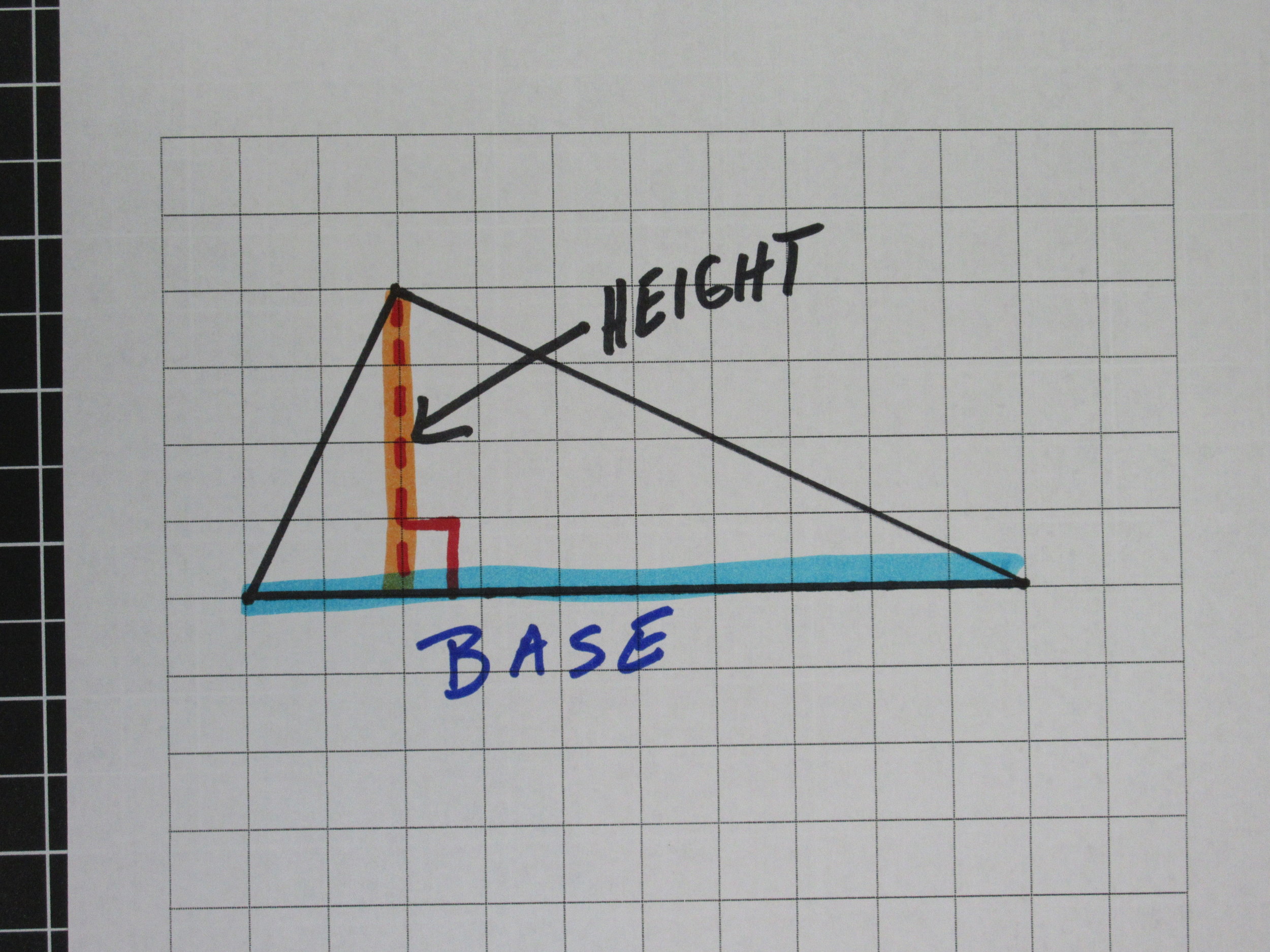
There are two key terms when working with triangles: Base and Height. The Base can be any of the three sides of the triangle. Generally, the base is the side of the triangle that is on the "bottom" or the side the triangle is resting on. You can rotate a triangle to make different sides be the base. This can be beneficial depending on which numbers are given/known.

The Height of a triangle is the distance from the base straight up (perpendicular) to its highest point. Below are a few examples of base and height of a triangle. (Students will have the most trouble understanding the third example when the height is outside of the triangle)

Below is an example of turning a triangle to make the base a different side.

Formulas for Area of a Triangle

There are two formulas that we use to find the area of a triangle:

Base x Height divided by 2 or
(1/2) x Base x Height

These two formulas are the same. How can that be you might ask. When we multiply a number by 1/2 or divide a number by 2 we get the same answer. For example, if we multiply the number 8 by 1/2 we get 4 or if we take the same number (8) and divide it by 2 we also get 4. The result is the exactly the same.

Why these two formulas?

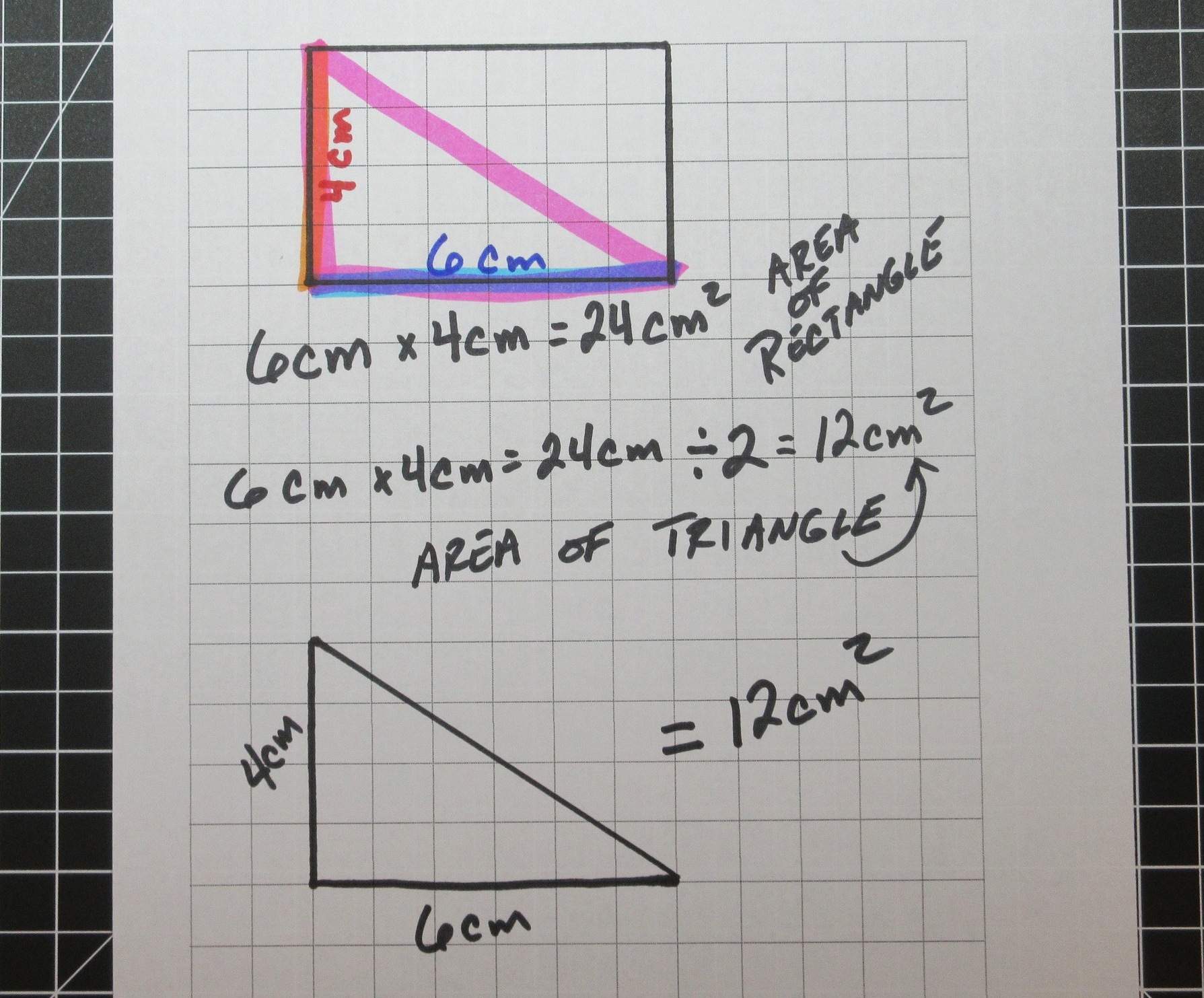
If you look at the following rectangle it has a base of 6 cm and a height of 4 cm with an area of 24 square cm.

By drawing a line diagonally through the rectangle we create a triangle with the same base (6 cm) and height (4 cm). When we look at the area of this triangle created, it's half of the area of the rectangle.

By multiplying the rectangles area by 1/2 or dividing it by 2 you get the area of the triangle.

Modeling Finding Area of Triangles

If you want to model finding the area of triangles you can take your triangle and rearrange it to form a rectangle which is easier to visualize the area. Below are a couple examples.

In this first example, we have a triangle with a base of 8 cm and a height of 4 cm. Below you can see that if we cut the base in half and rearrange we create a rectangle with a base of 4 (half of the original triangle) and a height of 4 (same as the triangle). It's easy to visualize how this triangle has an area of 16 square centimeters.

In this second example, we have a triangle with a base of 10 cm and a height of 10 cm. Below you can see that if we cut the base in half and rearrange we create a rectangle with a base of 5 (half of the original triangle) and a height of 10 (same as the triangle). It's easy to visualize how this triangle has an area of 50 square centimeters.

In the final example, we have a triangle with a base of 10 cm and a height of 4 cm. Because the height is not centered over the base we are going to cut our base two times. The orange line (which shows the height) visually divides our triangle into two smaller triangles. What we are going to do is cut each of these smaller triangles in half and then rearrange. When we do this we create a rectangle with a base of 5 (half the original) and a height of 4 (same as the orignal). It's easy to visualize how this triangle has an area of 20 square centimeters.

Examples of Calculating Area of Triangles (both formulas)

Below are 3 different examples of finding area of Triangles. In all three examples which show both formulas to calculate the area.

In this first example we have a base of 8 cm and a height of 3 cm. Our first option is to multiply 8 x 3 which equals 24. Then divide 24 by 2 which equals 12 square cm. The second option is to multiply 1/2 x 8 which is 4 then multiply that by 3 which also equals 12 square cm.

In the second example we have a base of 12 cm and a height of 4 cm. Our first option is to multiply 12 x 4 which equals 48. Then divide 48 by 2 which equals 24 square cm. The second option is to multiply 1/2 x 12 which is 6 then multiply that by 4 which also equals 24 square cm.

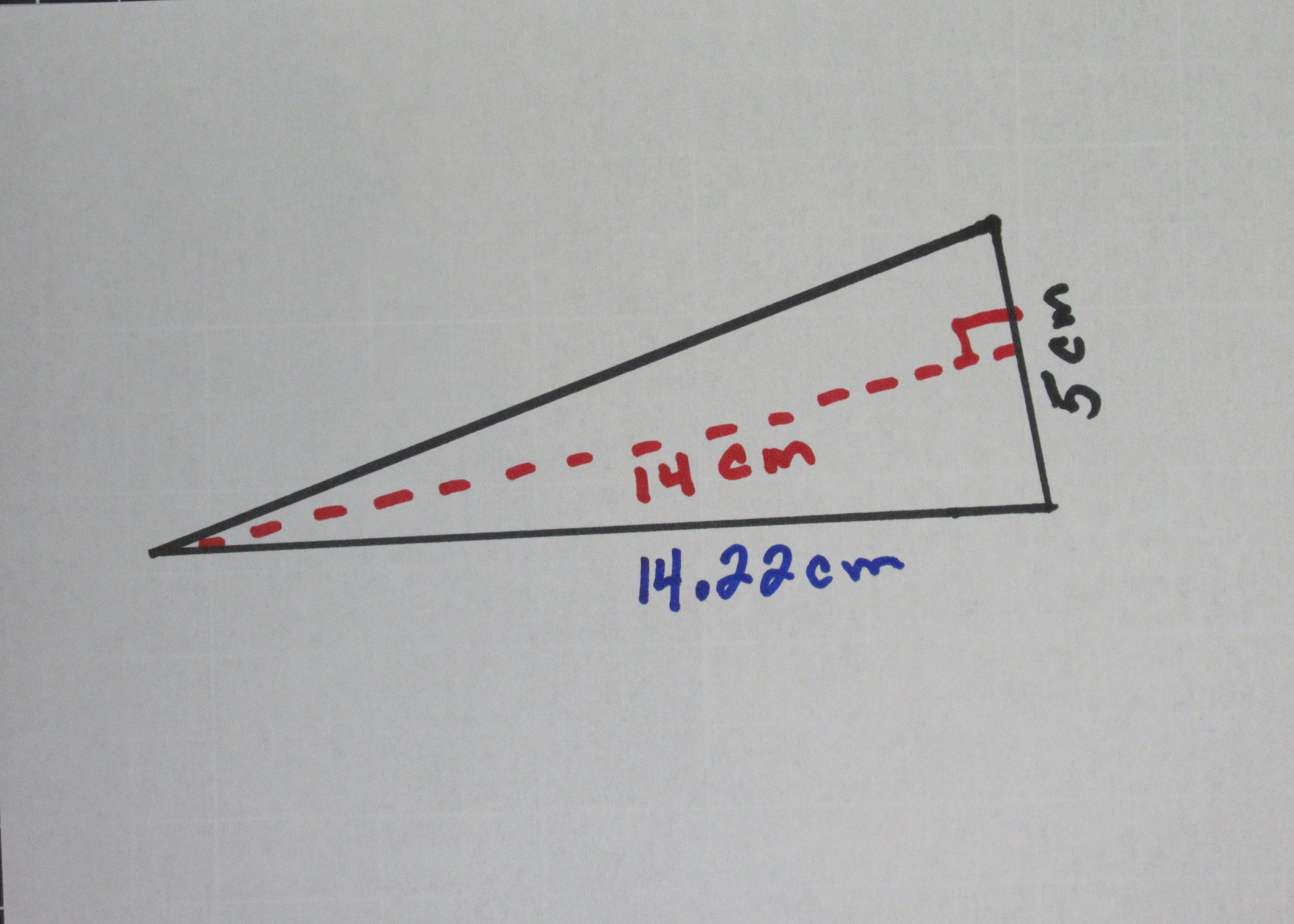
In the final example we have a base of 10 cm and a height of 4 cm (which is actually outside of the triangle). Our first option is to multiply 10 x 4 which equals 40. Then divide 40 by 2 which equals 20 square cm. The second option is to multiply 1/2 x 10 which is 5 then multiply that by 4 which also equals 20 square cm.

Below is our YouTube video showing "Finding Area of Triangles." Also we have included a link to our book "Finding Area of Unique Shapes" which uses area of triangles in many of the 44 different problems.