Area of Squares, Rectangles, Rhombuses, & Parallelograms
If you ever google: "How to find the area of a Square? Rectangle? Rhombus? or Parallelogram?" You are going to find a bunch of different answers.
For a Square, the formula given will be the Side Squared. The Rectangle's formula given is Length x Width. To find the area of a Rhombus you are given two different formulas: Base x Height or Diagonal #1 x Diagonal #2 divided by 2. Finally, the Parallelogram's formula for area is Base x Height.
All of these formulas are obviously correct, but you can make your life much simpler (or at least your kids) just using one simple formula:
Base x Height.
How is this even possible? The reason it's possible is because all four objects are Parallelograms. For a lot of students, it doesn't make sense how a Square, Rectangle and Rhombus are also Parallelograms. Below are the rules for an object to qualify as a Parallelogram.
Must have 4 sides
All 4 sides must be straight
Opposite sides must be the same length
Opposite sides must be parallel (so there are two sets of parallel sides)
Opposite angles must be the same
To the right we can see that the Square, Rhombus, and Rectangle each have a total of four sides and each of the sides are straight lines.
The blue and orange highlighted sides are parallel with each other. So each object has a total of two sets of parallel sides.
The green arcs (angles) are opposite of each other. These two angles are the same. In the Square and Rectangle all the angles are 90 degrees, but in the Rhombus the two opposite green angles are both acute angles (less than 90 degrees).
Opposite black arcs (angles) are also the same. In the Rhombus the opposite blacks arcs are each obtuse angles.
Because all 4 shapes (square, rectangle, rhombus & parallelogram) are parallelograms we can just use BASE x HEIGHT to find the area of all four of these shapes.
Modeling Area of Parallelograms
Squares and Rectangles are the two easiest shapes to model. Grid paper is a very easy way to show this to students.
On both of these images not only can you see the base and height but you can visualize the individual squares that make up the rectangle and square. So when we say the area of the rectangle is 10 cm squared we can see 10 squares that have sides that are each 1 cm
Modeling with Cheez-its
An easy way to engage students is to use Cheez-its (or other square food items like Starburst) when modeling. It's a simple way to turn this into a hands on lesson and the kids like the payoff at the end.
Modeling a Rhombus or Parallelogram (non square/rectangle)
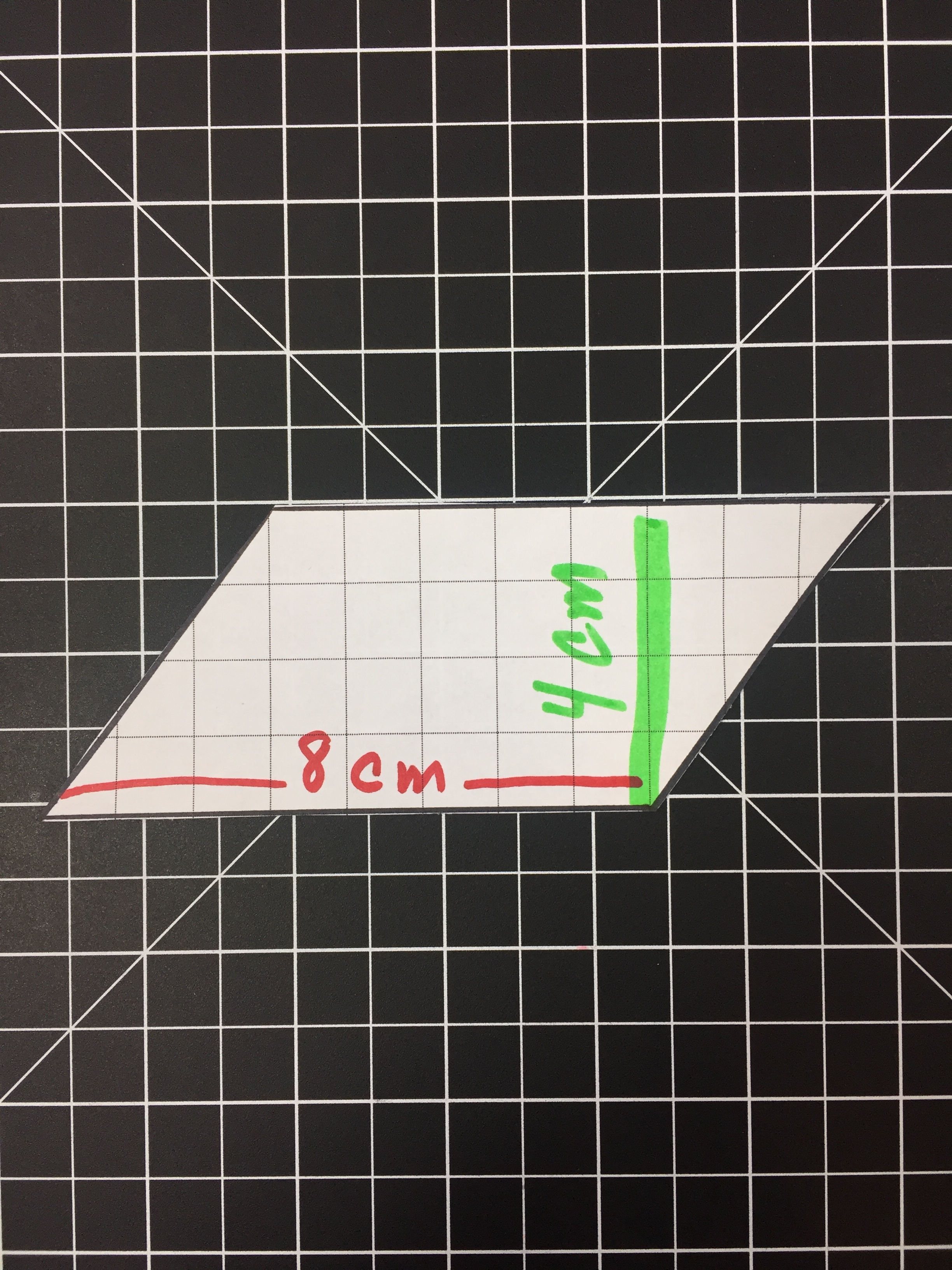
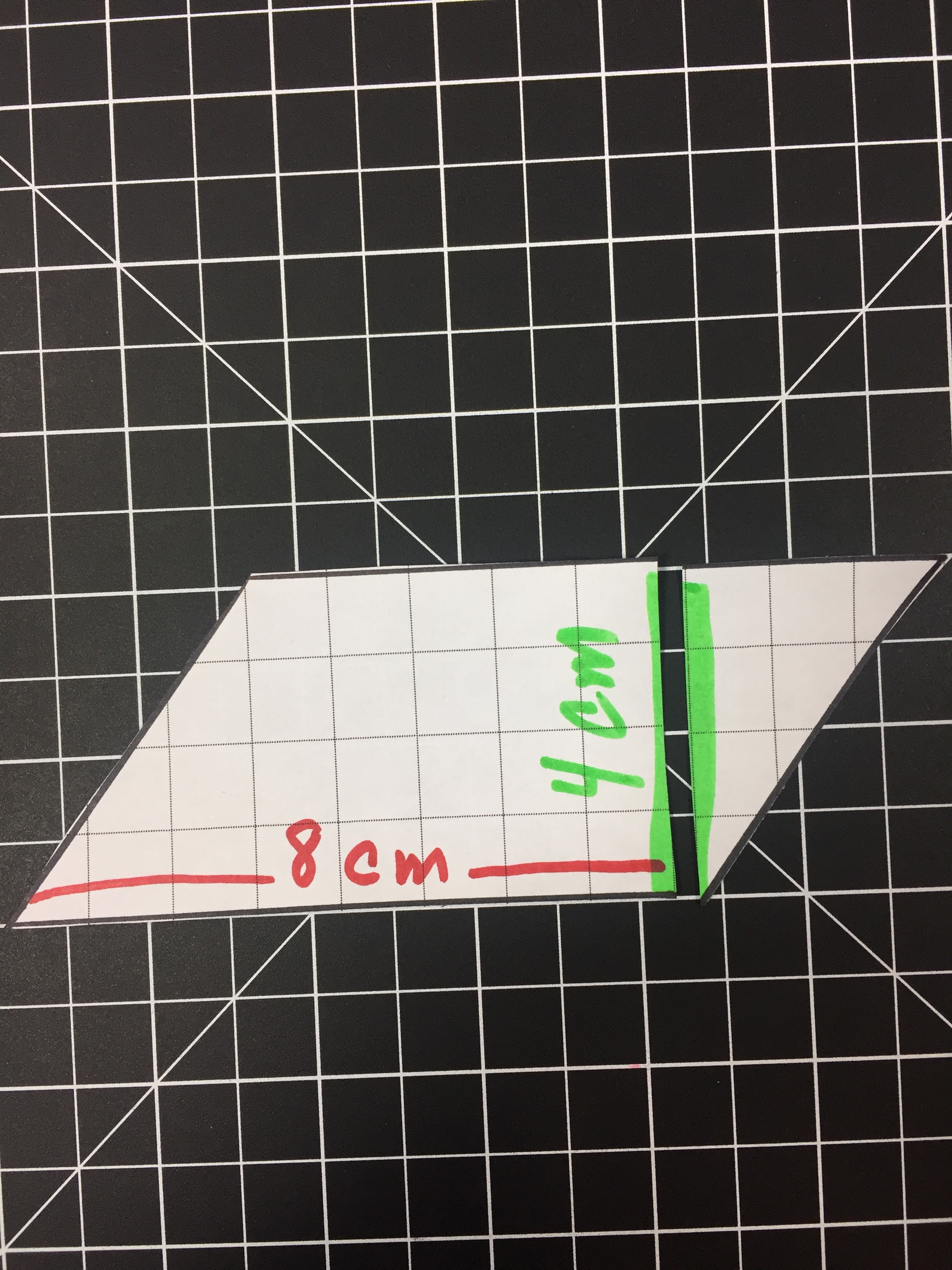
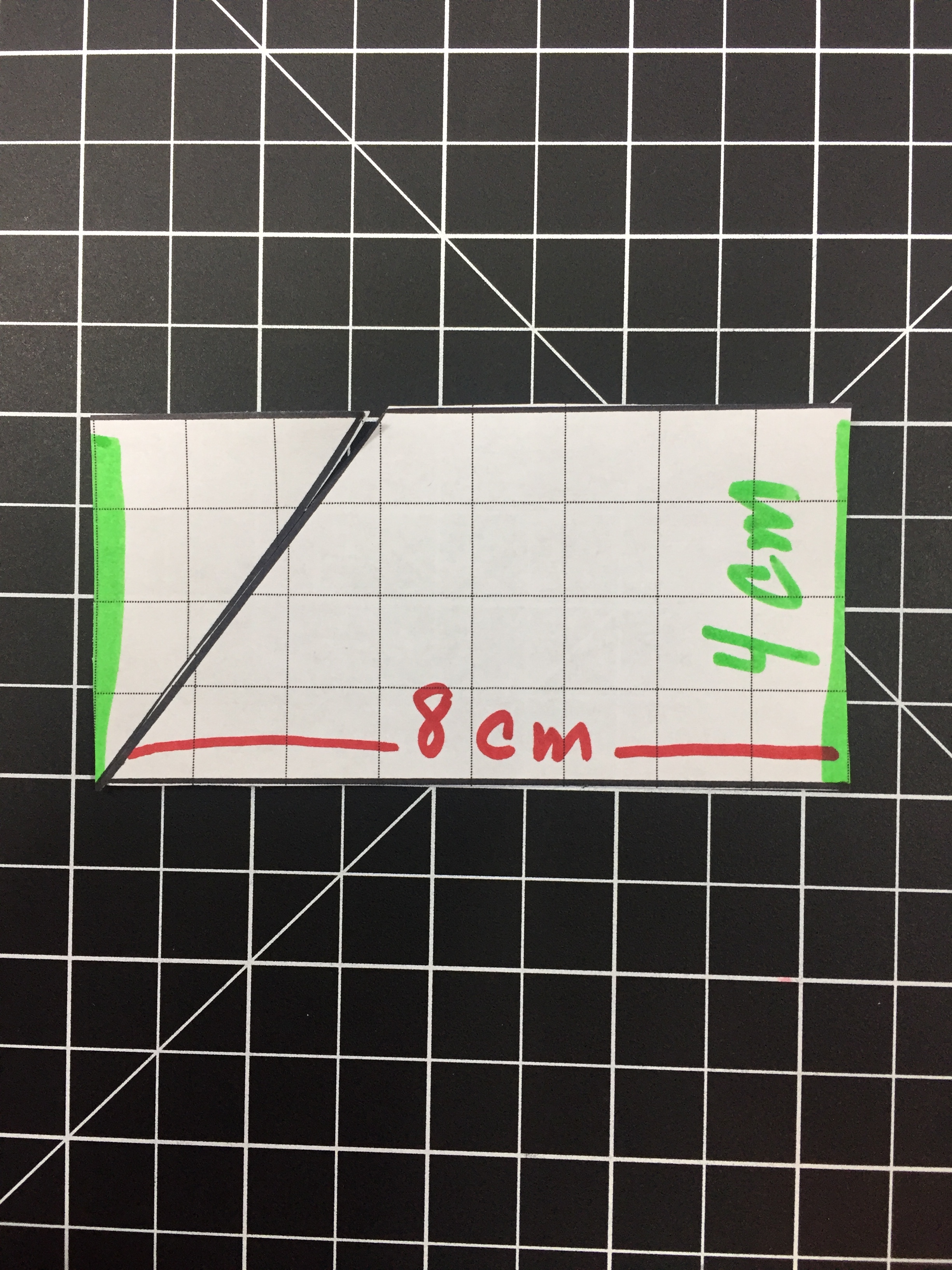
Modeling the area of a Rhombus or parallelogram is a bit harder with cheez-its (cutting up a cheez-its = pure mess). But it is fairly easy to model with grids. We can even turn the grids into a hands on lesson.
Below we have a Parallelogram (base of 8 with a height of 4) and cut it into two pieces by cutting on the height. We can rearrange the two sections to form a rectangle with a base of 8 and a height of 4 (same dimensions as before). By rearranging the Parallelogram we can visualize the 32 squares that make up the area
Below is another example of a parallelogram. We can take this parallelogram with a base of 10 and a height of 3 and cut into two parts by cutting on the height line. The two sections can be rearranged to form a rectangle with a base of 10 and a height of 3. By rearranging the Parallelogram we can visualize the 30 squares that make up the area.
We can model a Rhombus the exact same way by cutting into two parts (along the height) and then rearranging.
Length x Width vs. Base x Height
Is Length x Height the same as Base x Height?
The answer is Yes (sort of). It all depends on your perspective. On the image below left we are looking down on the rectangle. So, we would refer to these dimensions as the length and the width.
On the image below right we have changed our perspective of the rectangle. We are now looking straight ahead, so our dimensions are now base and height.
So Base and Length and Height and Width are basically the same.
When looking down on a rectangle we can see length and width.
When the same rectangle is upright (like above) we can visualize the height and base.
We hope you found this article helpful. You can follow us on:
Instagram, Pinterest, Twitter and YouTube at @landofmath
If you are looking for a more challenging activity for you kids check out "Finding Area of Unique Shapes" on Amazon.
This is a collection of 44 different shape combinations using rectangles, triangles, trapezoids, and circles.
The shapes progress in their difficulty.
You can check a video preview of this product below.