Cereal Box Project: A middle school math project (Copy)
For over a decade the Cereal Box Project has been a staple in our classroom. The idea is that a cereal box company is introducing a new cereal and they want a unique design for the cereal box to help gain extra attention.
Because the company wants something creative, a simple rectangular prism simply just won't do. The goal is for students to find ways to combine different shapes together to create this eye catching cereal box.
The following is a basic outline of the steps that we follow with this project. In addition, I'm including a few lessons from this years Cereal Box Project experience.
Step 1 - Come up with an Idea
The idea? A light bulb of course. How do you make a light bulb? Make a Hendecagon of naturally.
Like baseball? Really into Star Wars? Love doughnuts?
When coming up with an idea I find it helps student engagement when the students can use a topic that they are interested in. For example, if a student is really into baseball/softball they can make their cereal box look like a glove, bat, baseball field, home plate etc. This year a lot of my students are into the video game Fortnite. As a result, a large amount of cereal boxes has a strong Fortnite theme.
Step 2 - Reverse Engineer
As a middle school or elementary student there are certain limitations that we must work around. Many of these limitations are related to curves. For example, If you are trying to make a basketball (sphere), Football (prolate spheroid), or perhaps a megaphone (truncated cone) you are going to dive into a lot of math that is above middle school math level.
Have the students think about what they want to create and how they can arrange different shapes to make this object. For me, the fun and challenging part of the project is to create these difficult shapes by using the students current knowledge and skills.
Step 3 - Sketch out the idea
Put it down on paper. Draw the different shapes you are going to combine together to create your shape. Include dimensions.
Step 4 - Build a Prototype
I have our students build their prototype the same size as their actual project. We use scrap paper and masking tape to build these prototypes. A lot of potential pitfalls can be avoided during this step.
Step 5 - Cutting out individual Pieces
When you begin to build your actual Cereal Box the first thing I like for students to do is cut out the individual sides. We build our cereal boxes out of card stock which is a real thick paper similar to poster board. The thicker paper is nice because it is more stable.
Step 6 - Decorate the individual Pieces
Before the students begin to assemble their projects they should first decorate. Every year I will have a small collection of students that will tape their entire box together then decide to color and design it. This almost always leads to frustration and crushed cereal boxes.
Step 7 - Assemble the Cereal Box
We use scotch tape on the final project. We try to tape as much on the inside as possible. As a general rule: The less tape you see the better the project will look.
Step 8 - Complete the required paperwork
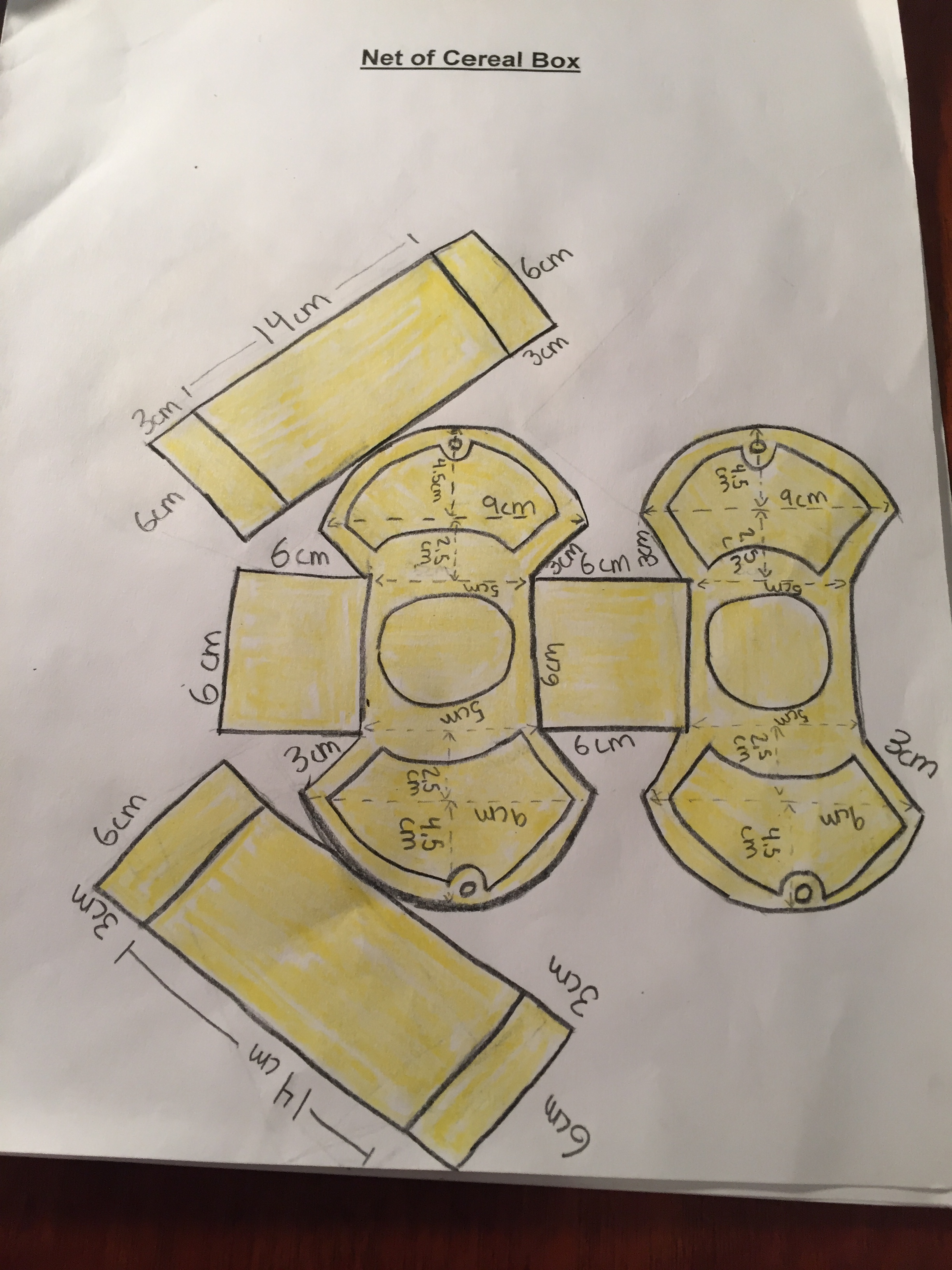
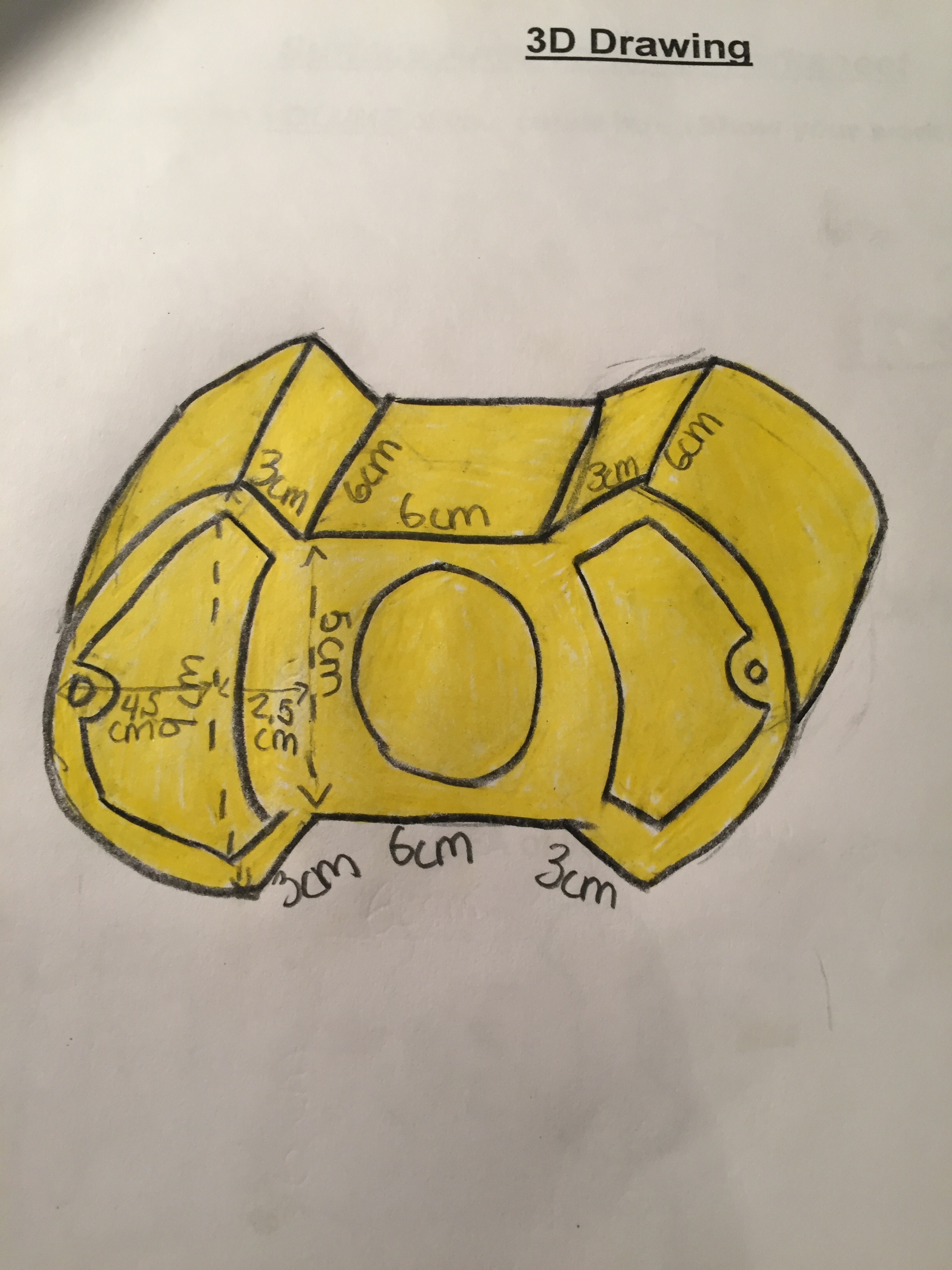
We usually have students calculate the surface area and volume of their projects. In addition we also have students draw (to scale) Nets and 3D designs of the project.
Lessons Learned from this years Cereal Box Projects
We had another successful year with our cereal box project. Many of the projects were creative and well done. Most of the students were fully engaged in the project. But we did have a couple areas that I need to clean up before next year.
The Curse of the Circle
We had a few students this year build cereal boxes that were either cylinders or had a circle as part of the design. In both of these cases many students just randomly made a circle and just wrapped a long stretch of paper around the circle. There was no thought given to diameter, radius, or circumference. Needless to say, this made for a mess when it came time to make the cereal box the same as its prototype and with calculating surface area and volume.
Struggles with Scissors and Straight lines
Normally I will take a day (or two) to show the students a few tips/tricks when making and cutting out the sides of their project. Because of a time crunch this year, I thought I could save a little time and just give a brief talk and turn them lose. In the end this just created a lot more work for me and made it harder to help out as many students.
Interested in giving the Cereal Box Project a try?
This book will give you an in depth guide to how I use this project in my class.
Area of Trapezoids made easy.
In the world of quadrilaterals, the formula to find area of Trapezoids is one of the most feared by middle school students. Perhaps it’s the use of parentheses. If you throw these bad boys into a problem it’s sure to create a certain level of anarchy. Possibly it’s the use of the numbers 1 and 2 written below and to the right of the two bases (b) in the parentheses.
Regardless of of the reason, the formula for Area of Trapezoids has caused many kids to surrender without so much as a fight.
The kicker is that the formula is not difficult to solve. In this blog we will look at a couple of the key terms, dissect the formula, give three examples of finding area and show you a three ways to model finding the area.
Above: Two different formulas to find Area of Trapezoids
The Trapezoid
In the world of quadrilaterals, the formula to find area of Trapezoids is one of the most feared by middle school students. Perhaps it’s the use of parentheses. If you throw these bad boys into a problem it’s sure to create a certain level of anarchy. Possibly it’s the use of the numbers 1 and 2 written below and to the right of the two bases (b) in the parentheses.
Regardless of of the reason, the formula for Area of Trapezoids has caused many kids to surrender without so much as a fight.
The kicker is that the formula is not difficult to solve. In this blog we will look at a couple of the key terms, dissect the formula, give three examples of finding area and show you a few ways to model finding the area.
Key Terms
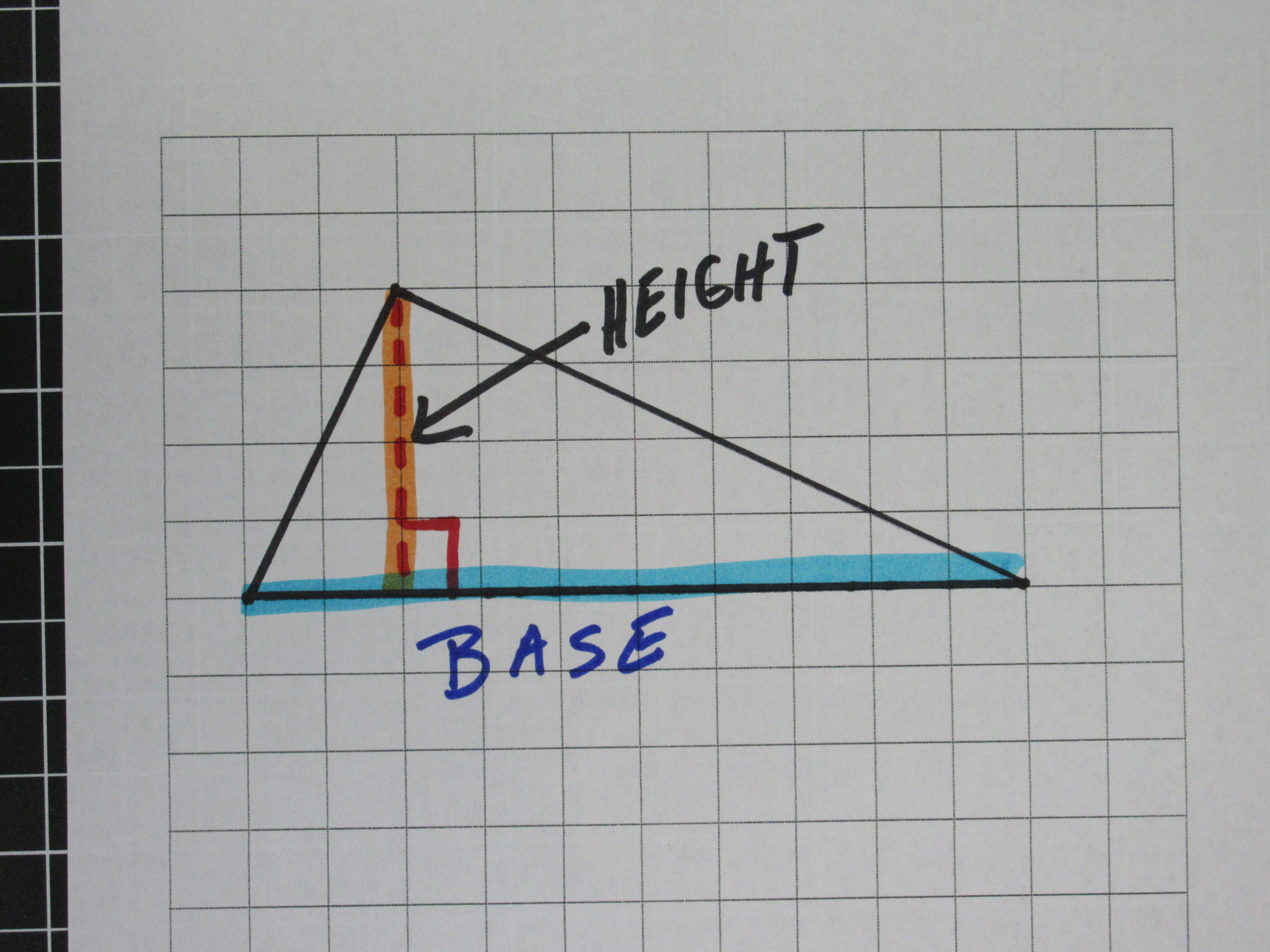
There are two key terms in the world of the Trapezoid: Bases and Height.
The Bases are two sides that are parallel. Trapezoids have only one set of parallel sides. The Height can also be thought of as the distance between the bases. In most examples, the two bases are on the top and the bottom, but if you rotate the trapezoid 90 degrees the bases are now on the right and left sides.
Area of Trapezoid Formula
There are two common formulas that you will see used when finding the area of a trapezoid:
Area = 1/2 (Base 1 + Base 2) x height or
Area = (Base 1 + Base 2) divided by 2 x height
It’s important to understand that dividing by 2 and multiplying by 1/2 are the same thing. For example, 10 divided by 2 equals 5 and 10 times 1/2 also equals 5.
What is helpful to understand is that 1/2 (Base 1 + Base 2) and (Base 1 + Base 2) divided by 2 are both just ways of finding the average of the two bases. You can think of this as the Mean or the Median it doesn’t matter. So really Area of a Trapezoid is just the Average of the Bases x Height (or the distance between the bases)
3 Examples of Finding area of Trapezoids
Example #1
In this example we have a trapezoid with a bases of 13 and 7 and a height of 3. First we add up our bases to get 20 (13 + 7). Next we multiply 20 by 1/2 to get 10. (We could have divided by 2 instead of multiplying by 1/2). Finally we take 10 (which is the average of the two bases) and multiply it by the height (3) to find the area of this trapezoid which is 30 square units.
Example #2
In this example we have a trapezoid with a bases of 10 and 6 and a height of 6. First we add up our bases to get 16 (10 + 6). Next we multiply 16 by 1/2 to get 8. (We could have divided by 2 instead of multiplying by 1/2). Finally we take 8 (which is the average of the two bases) and multiply it by the height (6) to find the area of this trapezoid which is 48 square units.
Example #3
In this example we have a trapezoid with a bases of 10 and 6 and a height of 3. First we add up our bases to get 16 (10 + 6). Next we multiply 16 by 1/2 to get 8. (We could have divided by 2 instead of multiplying by 1/2). Finally we take 8 (which is the average of the two bases) and multiply it by the height (3) to find the area of this trapezoid which is 24 square units.
3 Ways to model Finding the area of Trapezoids
Example #1
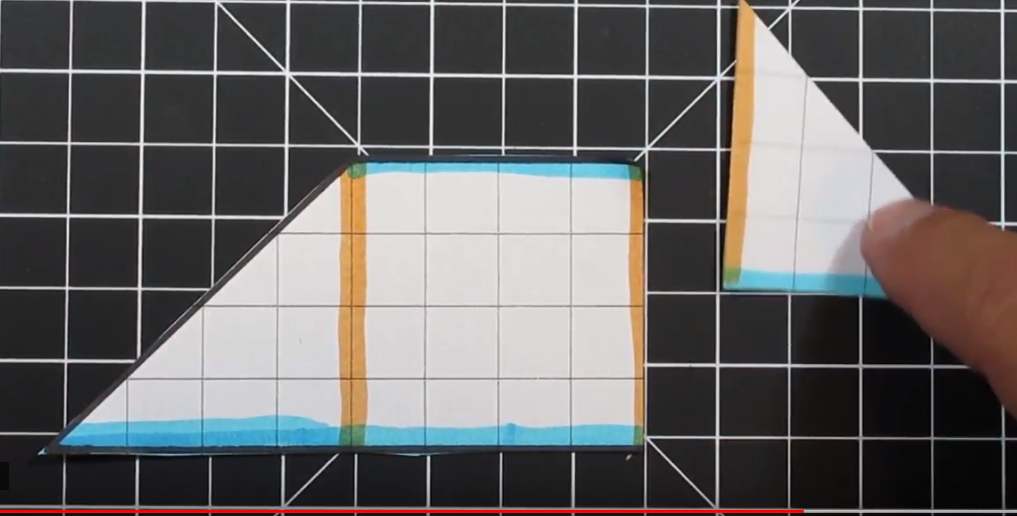
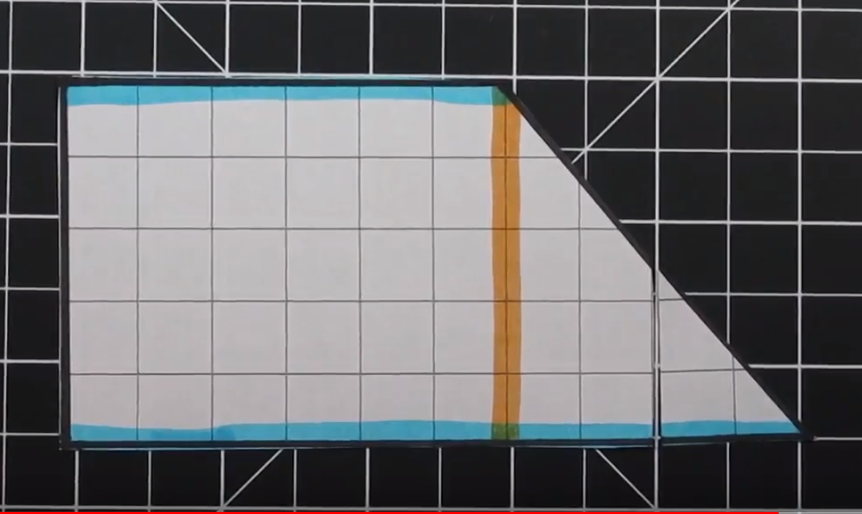
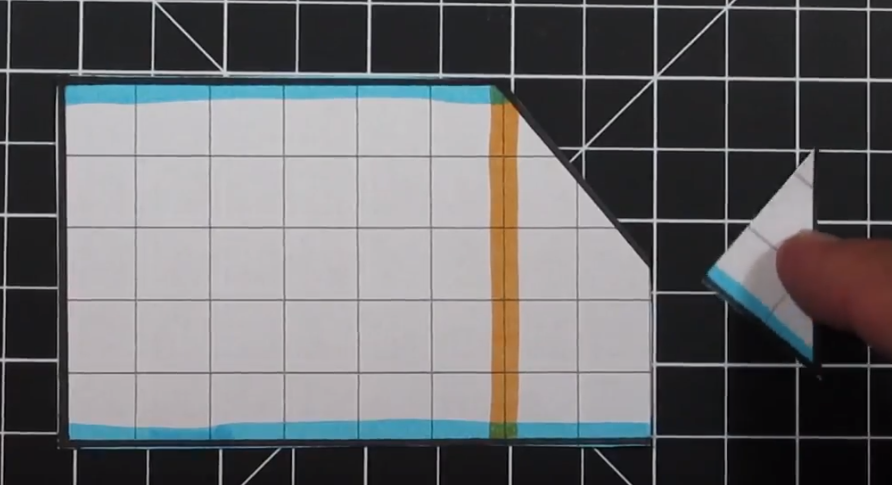
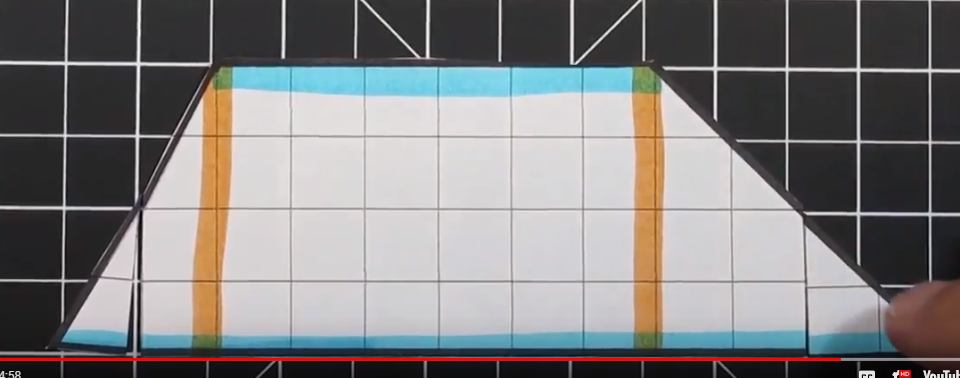
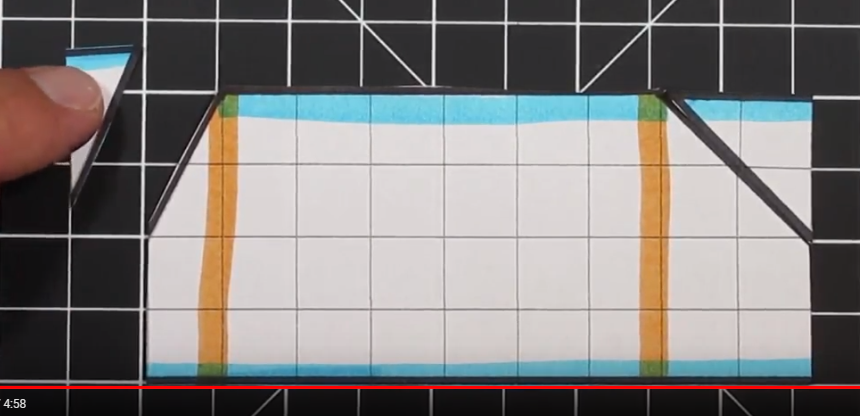
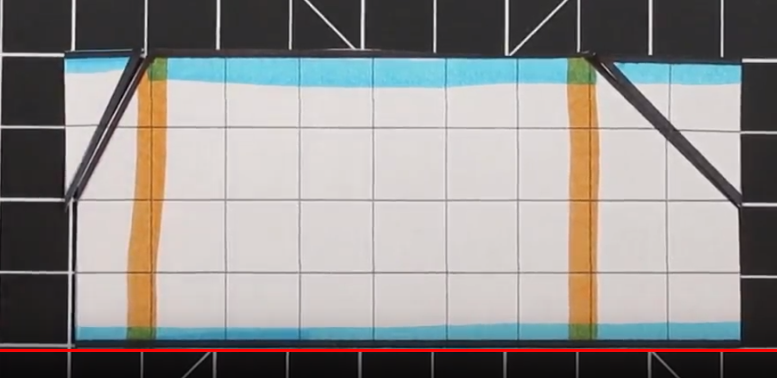
This is an example of a Trapezoid when the “triangles” are the same on both sides.
One of the goals of modeling area of a trapezoid is to show how we can convert a trapezoid into a rectangle. In the above example, we have two equal “triangles” on each side. This trapezoid has bases of 12 and 4 with a height of 4.
First, we can cut off one of the two triangles. We are then going to move it to the other side.
Once we move the triangle from one side to the other (in this example right to left) we can arrange the triangle to fit perfectly and form a rectangle. In this example an 8 x 4 rectangle is created which has an area of 32 units squared.
Example #2
This is an example of a trapezoid with two right angles. As a result there is only one “triangle.”
This Trapezoid has two right angles on the left side. There is a triangle on the right side. The Trapezoid has bases of 6 (on top) and 10 (bottom) along with a height of 5.
To transform this trapezoid into a rectangle we are going to cut the triangle in half (half of the base of the triangle). Next we are going to take the piece we cut off and move to the upper right to create a rectangle.
Finally, once we rearrange the trapezoid we can create a rectangle with a base of 8 and a height of 5. This equals an area of 40 cm squared.
Example #3
This an example of a trapezoid with triangles on each side, but both have a different base.
This trapezoid is similar to the trapezoid in Example #1. The big difference is the two triangles have a different base. So just like in Example 2, we are going to need to cut both triangles in half.
In this example, we are cutting the triangle on the right side in half and rearranging it .
Next, we do the same thing to the triangle on the left side.
Once we rearrange the trapezoid, a rectangle with a base of 9 and height of 4 has been created. The area is 36 square units which is easy to see when we rearrange the trapezoid.
Watch the Video !
Check out: Finding the Area of Unique Shapes.
A collection of 44 different Shapes using triangles, quadrilaterals (including trapezoids) and circles.
Area of Triangles
Finding area of Triangles can be challenging for students and parents alike. In this article, we break down the formula(s), show the reasoning behind area formulas, model and give examples of calculation the area.
Finding the Area of Triangles
One of the struggles every year for some middle school students is finding the Area of Triangles. In this blog we will look at a few ways to help explain the process and make it a bit easier.
Key Terms
There are two key terms when working with triangles: Base and Height. The Base can be any of the three sides of the triangle. Generally, the base is the side of the triangle that is on the "bottom" or the side the triangle is resting on. You can rotate a triangle to make different sides be the base. This can be beneficial depending on which numbers are given/known.
The Height of a triangle is the distance from the base straight up (perpendicular) to its highest point. Below are a few examples of base and height of a triangle. (Students will have the most trouble understanding the third example when the height is outside of the triangle)
Below is an example of turning a triangle to make the base a different side.
Formulas for Area of a Triangle
There are two formulas that we use to find the area of a triangle:
Base x Height divided by 2 or
(1/2) x Base x Height
These two formulas are the same. How can that be you might ask. When we multiply a number by 1/2 or divide a number by 2 we get the same answer. For example, if we multiply the number 8 by 1/2 we get 4 or if we take the same number (8) and divide it by 2 we also get 4. The result is the exactly the same.
Why these two formulas?
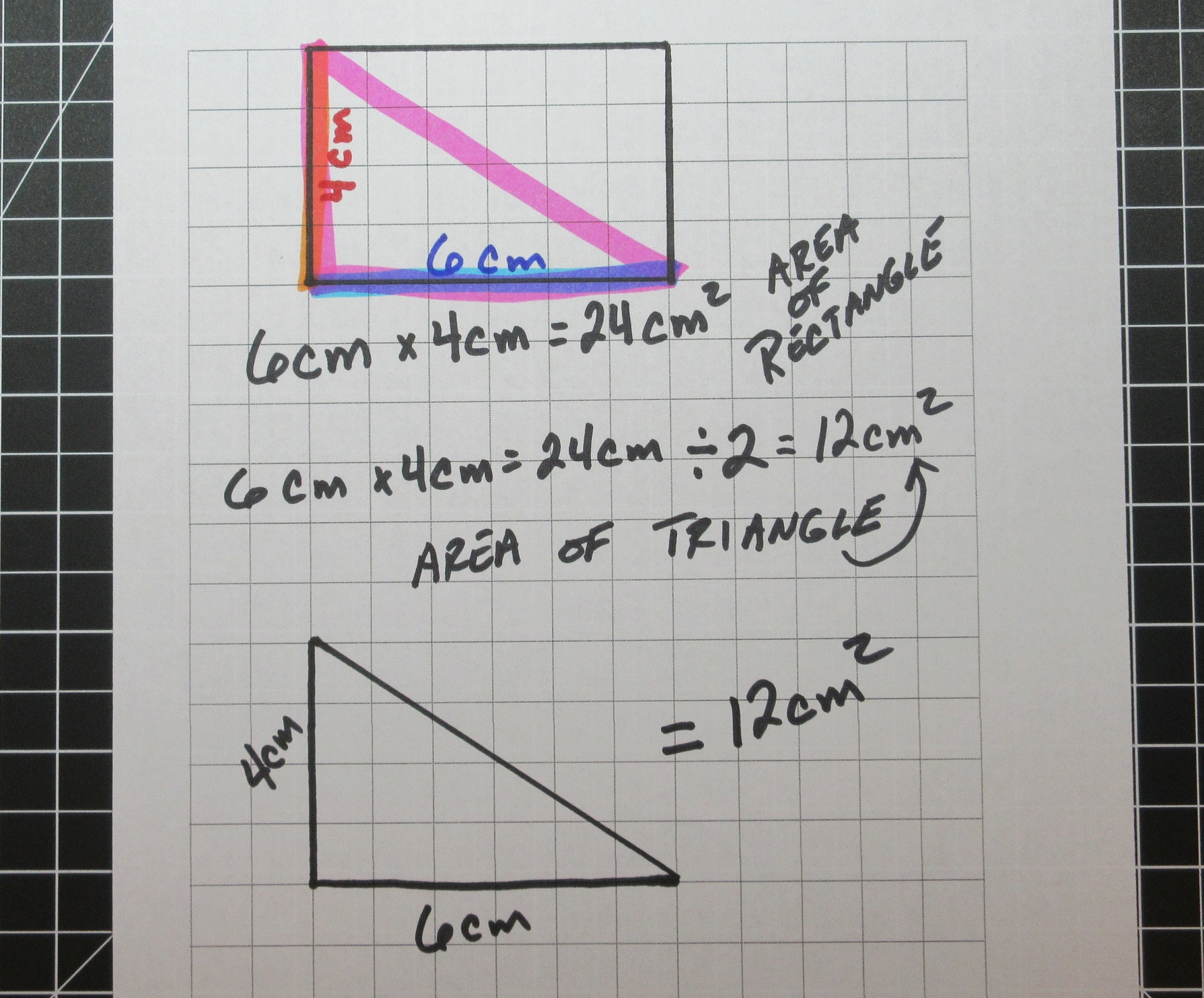
If you look at the following rectangle it has a base of 6 cm and a height of 4 cm with an area of 24 square cm.
By drawing a line diagonally through the rectangle we create a triangle with the same base (6 cm) and height (4 cm). When we look at the area of this triangle created, it's half of the area of the rectangle.
By multiplying the rectangles area by 1/2 or dividing it by 2 you get the area of the triangle.
Modeling Finding Area of Triangles
If you want to model finding the area of triangles you can take your triangle and rearrange it to form a rectangle which is easier to visualize the area. Below are a couple examples.
In this first example, we have a triangle with a base of 8 cm and a height of 4 cm. Below you can see that if we cut the base in half and rearrange we create a rectangle with a base of 4 (half of the original triangle) and a height of 4 (same as the triangle). It's easy to visualize how this triangle has an area of 16 square centimeters.
In this second example, we have a triangle with a base of 10 cm and a height of 10 cm. Below you can see that if we cut the base in half and rearrange we create a rectangle with a base of 5 (half of the original triangle) and a height of 10 (same as the triangle). It's easy to visualize how this triangle has an area of 50 square centimeters.
In the final example, we have a triangle with a base of 10 cm and a height of 4 cm. Because the height is not centered over the base we are going to cut our base two times. The orange line (which shows the height) visually divides our triangle into two smaller triangles. What we are going to do is cut each of these smaller triangles in half and then rearrange. When we do this we create a rectangle with a base of 5 (half the original) and a height of 4 (same as the orignal). It's easy to visualize how this triangle has an area of 20 square centimeters.
Examples of Calculating Area of Triangles (both formulas)
Below are 3 different examples of finding area of Triangles. In all three examples which show both formulas to calculate the area.
In this first example we have a base of 8 cm and a height of 3 cm. Our first option is to multiply 8 x 3 which equals 24. Then divide 24 by 2 which equals 12 square cm. The second option is to multiply 1/2 x 8 which is 4 then multiply that by 3 which also equals 12 square cm.
In the second example we have a base of 12 cm and a height of 4 cm. Our first option is to multiply 12 x 4 which equals 48. Then divide 48 by 2 which equals 24 square cm. The second option is to multiply 1/2 x 12 which is 6 then multiply that by 4 which also equals 24 square cm.
In the final example we have a base of 10 cm and a height of 4 cm (which is actually outside of the triangle). Our first option is to multiply 10 x 4 which equals 40. Then divide 40 by 2 which equals 20 square cm. The second option is to multiply 1/2 x 10 which is 5 then multiply that by 4 which also equals 20 square cm.
Below is our YouTube video showing "Finding Area of Triangles." Also we have included a link to our book "Finding Area of Unique Shapes" which uses area of triangles in many of the 44 different problems.
Area of Squares, Rectangles, Rhombuses, & Parallelograms
If you ever google: "How to find the area of a Square? Rectangle? Rhombus? or Parallelogram?" You are going to find a bunch of different answers.
For a Square, the formula given will be the Side Squared. The Rectangle's formula given is Length x Width. To find the area of a Rhombus you are given two different formulas: Base x Height or Diagonal #1 x Diagonal #2 divided by 2. Finally, the Parallelogram's formula for area is Base x Height.
All of these formulas are obviously correct, but you can make your life much simpler (or at least your kids) just using one simple formula:
Base x Height.
How is this even possible? The reason it's possible is because all four objects are Parallelograms. For a lot of students, it doesn't make sense how a Square, Rectangle and Rhombus are also Parallelograms. Below are the rules for an object to qualify as a Parallelogram.
Must have 4 sides
All 4 sides must be straight
Opposite sides must be the same length
Opposite sides must be parallel (so there are two sets of parallel sides)
Opposite angles must be the same
To the right we can see that the Square, Rhombus, and Rectangle each have a total of four sides and each of the sides are straight lines.
The blue and orange highlighted sides are parallel with each other. So each object has a total of two sets of parallel sides.
The green arcs (angles) are opposite of each other. These two angles are the same. In the Square and Rectangle all the angles are 90 degrees, but in the Rhombus the two opposite green angles are both acute angles (less than 90 degrees).
Opposite black arcs (angles) are also the same. In the Rhombus the opposite blacks arcs are each obtuse angles.
Because all 4 shapes (square, rectangle, rhombus & parallelogram) are parallelograms we can just use BASE x HEIGHT to find the area of all four of these shapes.
Modeling Area of Parallelograms
Squares and Rectangles are the two easiest shapes to model. Grid paper is a very easy way to show this to students.
On both of these images not only can you see the base and height but you can visualize the individual squares that make up the rectangle and square. So when we say the area of the rectangle is 10 cm squared we can see 10 squares that have sides that are each 1 cm
Modeling with Cheez-its
An easy way to engage students is to use Cheez-its (or other square food items like Starburst) when modeling. It's a simple way to turn this into a hands on lesson and the kids like the payoff at the end.
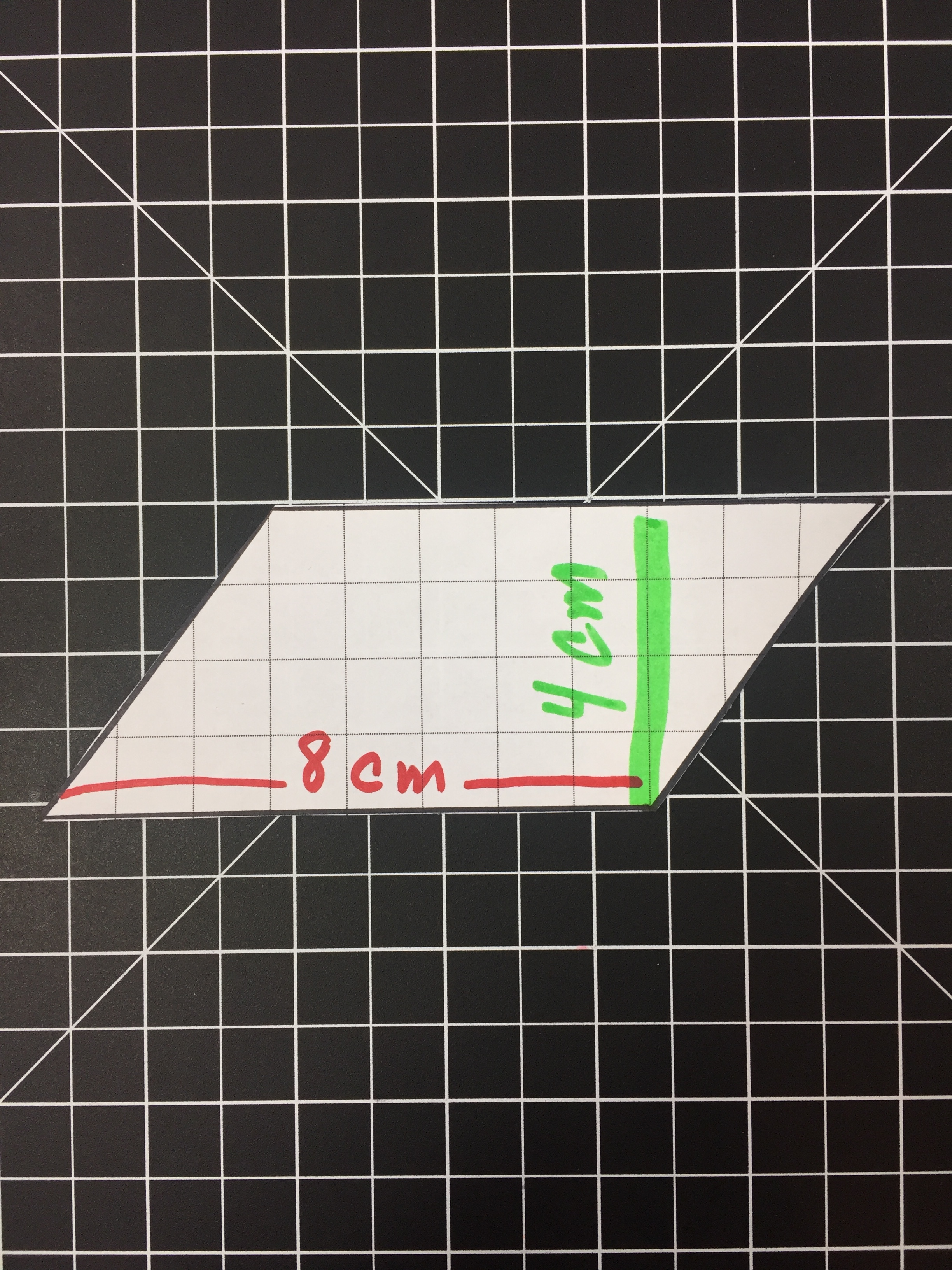
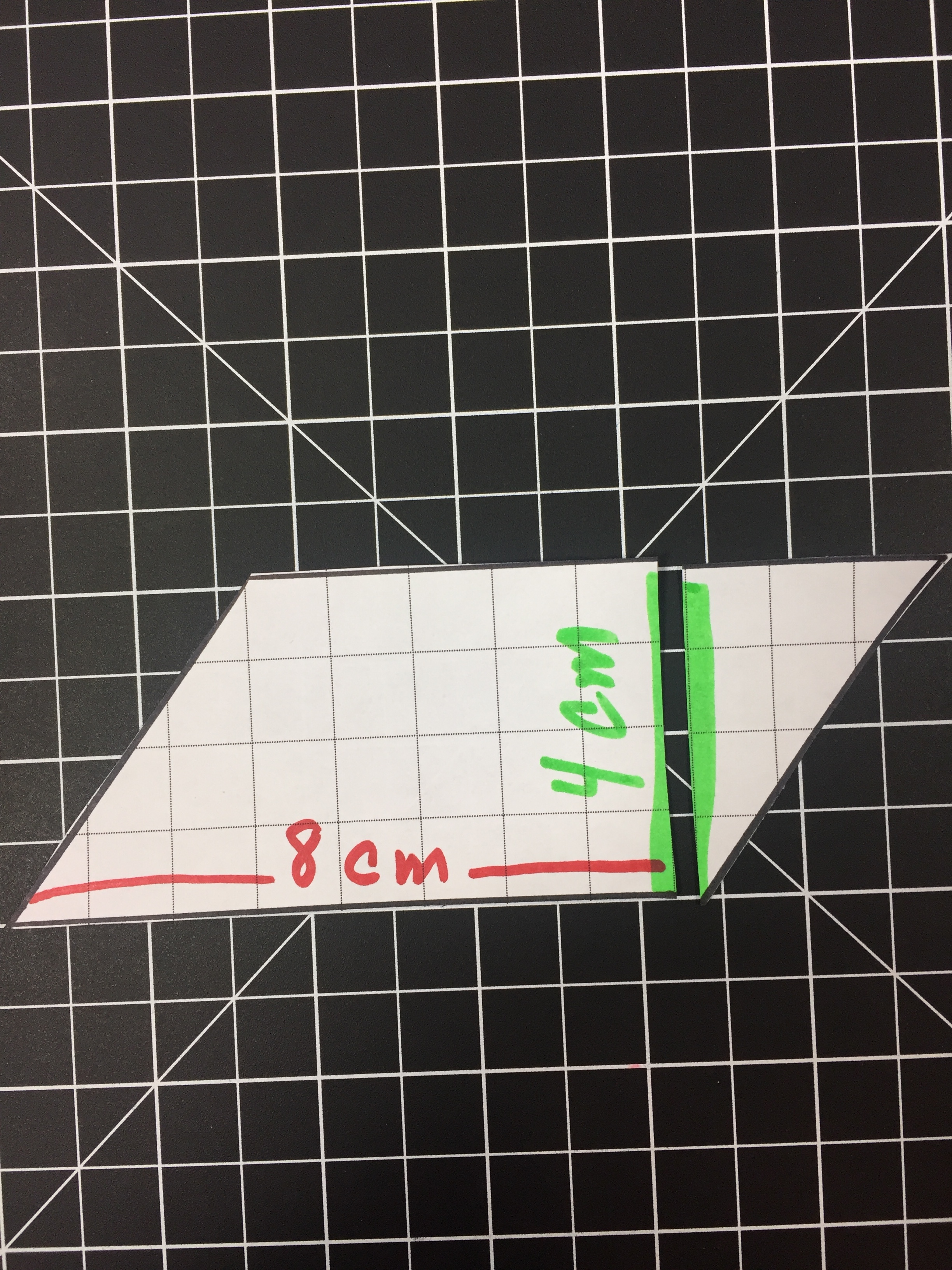
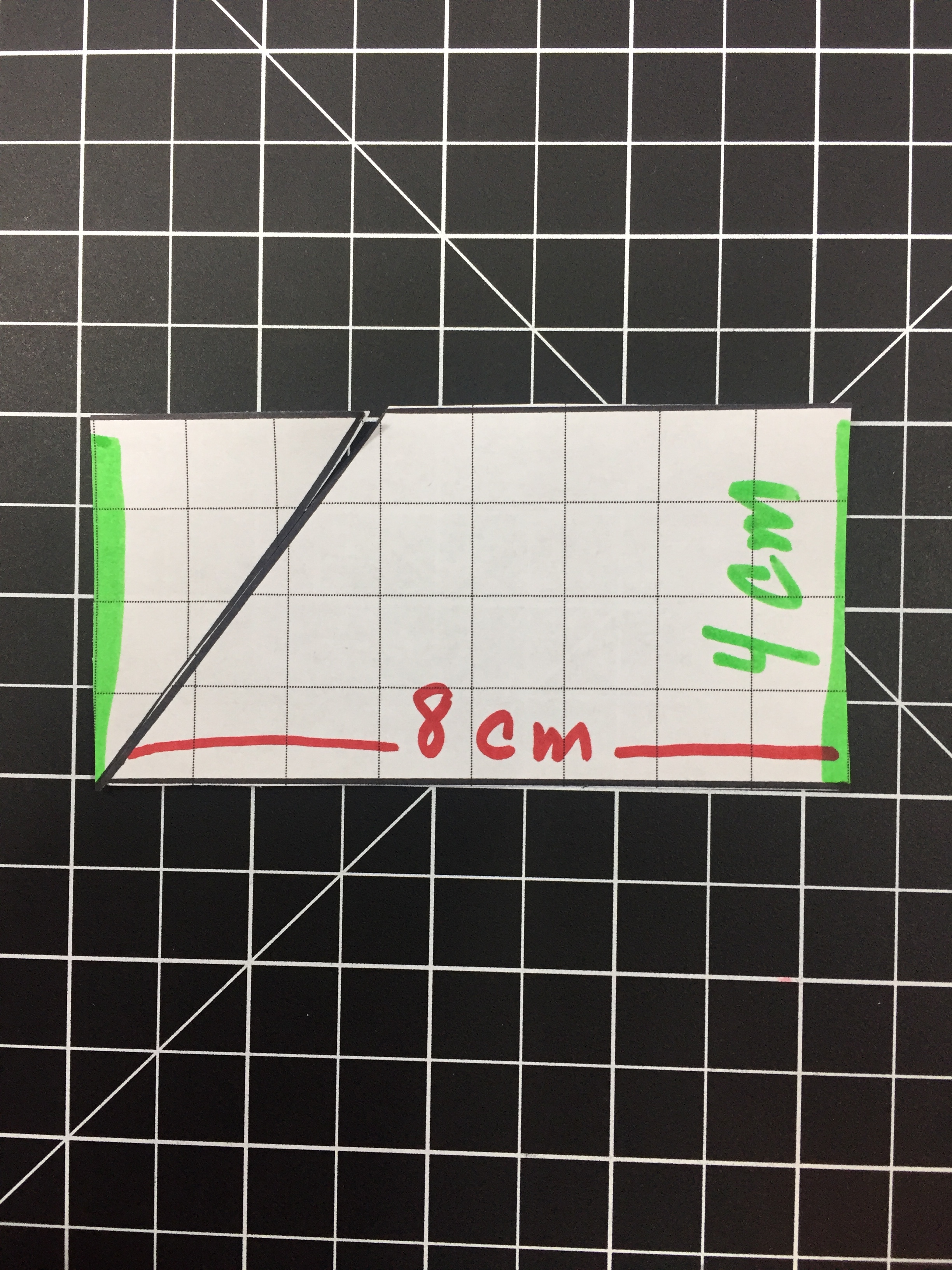
Modeling a Rhombus or Parallelogram (non square/rectangle)
Modeling the area of a Rhombus or parallelogram is a bit harder with cheez-its (cutting up a cheez-its = pure mess). But it is fairly easy to model with grids. We can even turn the grids into a hands on lesson.
Below we have a Parallelogram (base of 8 with a height of 4) and cut it into two pieces by cutting on the height. We can rearrange the two sections to form a rectangle with a base of 8 and a height of 4 (same dimensions as before). By rearranging the Parallelogram we can visualize the 32 squares that make up the area
Below is another example of a parallelogram. We can take this parallelogram with a base of 10 and a height of 3 and cut into two parts by cutting on the height line. The two sections can be rearranged to form a rectangle with a base of 10 and a height of 3. By rearranging the Parallelogram we can visualize the 30 squares that make up the area.
We can model a Rhombus the exact same way by cutting into two parts (along the height) and then rearranging.
Length x Width vs. Base x Height
Is Length x Height the same as Base x Height?
The answer is Yes (sort of). It all depends on your perspective. On the image below left we are looking down on the rectangle. So, we would refer to these dimensions as the length and the width.
On the image below right we have changed our perspective of the rectangle. We are now looking straight ahead, so our dimensions are now base and height.
So Base and Length and Height and Width are basically the same.
When looking down on a rectangle we can see length and width.
When the same rectangle is upright (like above) we can visualize the height and base.
We hope you found this article helpful. You can follow us on:
Instagram, Pinterest, Twitter and YouTube at @landofmath
If you are looking for a more challenging activity for you kids check out "Finding Area of Unique Shapes" on Amazon.
This is a collection of 44 different shape combinations using rectangles, triangles, trapezoids, and circles.
The shapes progress in their difficulty.
You can check a video preview of this product below.
Cereal Box Project: A middle school math project
For over a decade the Cereal Box Project has been a staple in our classroom. The idea is that a cereal box company is introducing a new cereal and they want a unique design for the cereal box to help gain extra attention.
Because the company wants something creative, a simple rectangular prism simply just won't do. The goal is for students to find ways to combine different shapes together to create this eye catching cereal box.
The following is a basic outline of the steps that we follow with this project. In addition, I'm including a few lessons from this years Cereal Box Project experience.
Step 1 - Come up with an Idea
The idea? A light bulb of course. How do you make a light bulb? Make a Hendecagon of naturally.
Like baseball? Really into Star Wars? Love doughnuts?
When coming up with an idea I find it helps student engagement when the students can use a topic that they are interested in. For example, if a student is really into baseball/softball they can make their cereal box look like a glove, bat, baseball field, home plate etc. This year a lot of my students are into the video game Fortnite. As a result, a large amount of cereal boxes has a strong Fortnite theme.
Step 2 - Reverse Engineer
As a middle school or elementary student there are certain limitations that we must work around. Many of these limitations are related to curves. For example, If you are trying to make a basketball (sphere), Football (prolate spheroid), or perhaps a megaphone (truncated cone) you are going to dive into a lot of math that is above middle school math level.
Have the students think about what they want to create and how they can arrange different shapes to make this object. For me, the fun and challenging part of the project is to create these difficult shapes by using the students current knowledge and skills.
Step 3 - Sketch out the idea
Put it down on paper. Draw the different shapes you are going to combine together to create your shape. Include dimensions.
Step 4 - Build a Prototype
I have our students build their prototype the same size as their actual project. We use scrap paper and masking tape to build these prototypes. A lot of potential pitfalls can be avoided during this step.
Step 5 - Cutting out individual Pieces
When you begin to build your actual Cereal Box the first thing I like for students to do is cut out the individual sides. We build our cereal boxes out of card stock which is a real thick paper similar to poster board. The thicker paper is nice because it is more stable.
Step 6 - Decorate the individual Pieces
Before the students begin to assemble their projects they should first decorate. Every year I will have a small collection of students that will tape their entire box together then decide to color and design it. This almost always leads to frustration and crushed cereal boxes.
Step 7 - Assemble the Cereal Box
We use scotch tape on the final project. We try to tape as much on the inside as possible. As a general rule: The less tape you see the better the project will look.
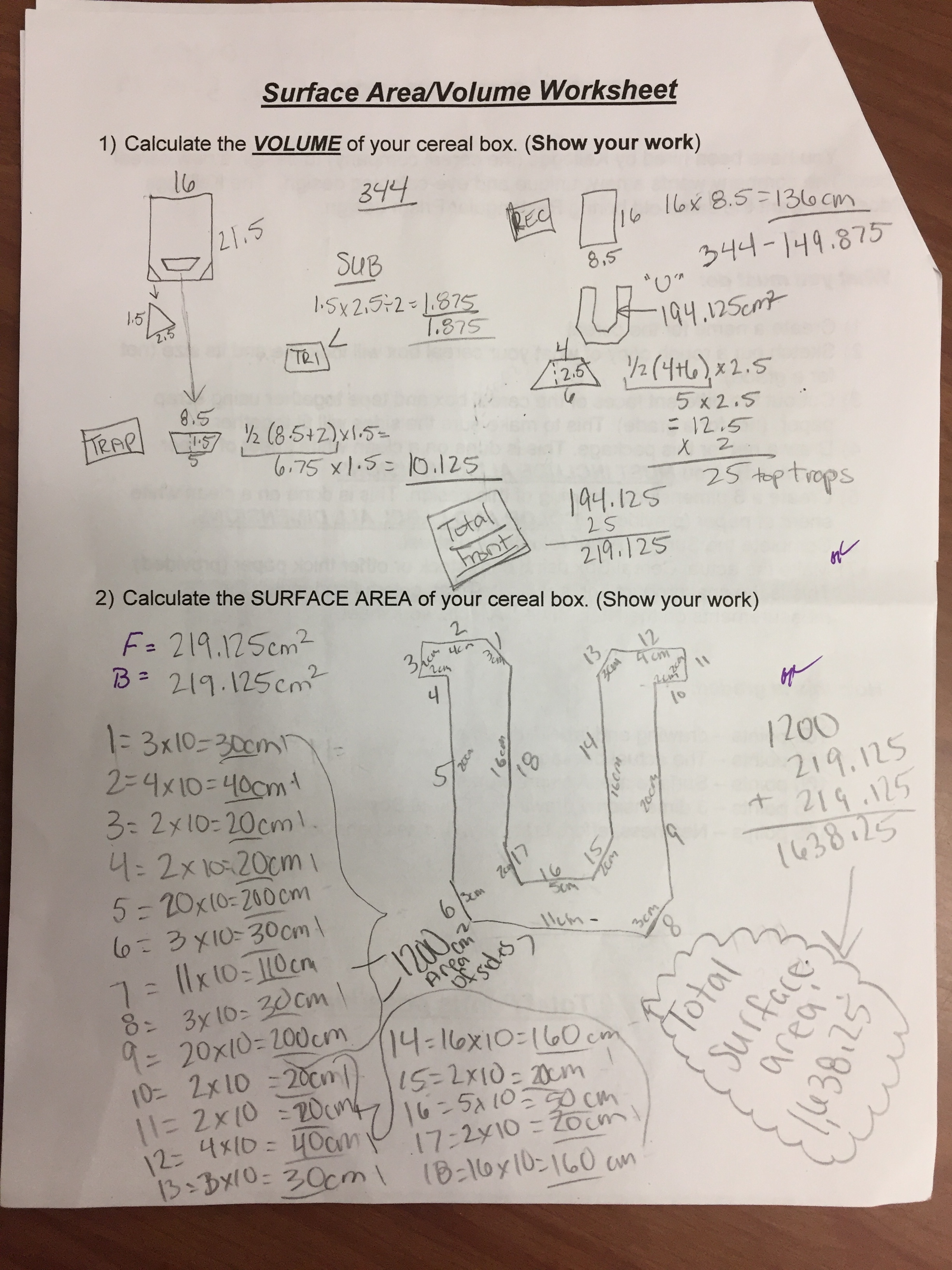
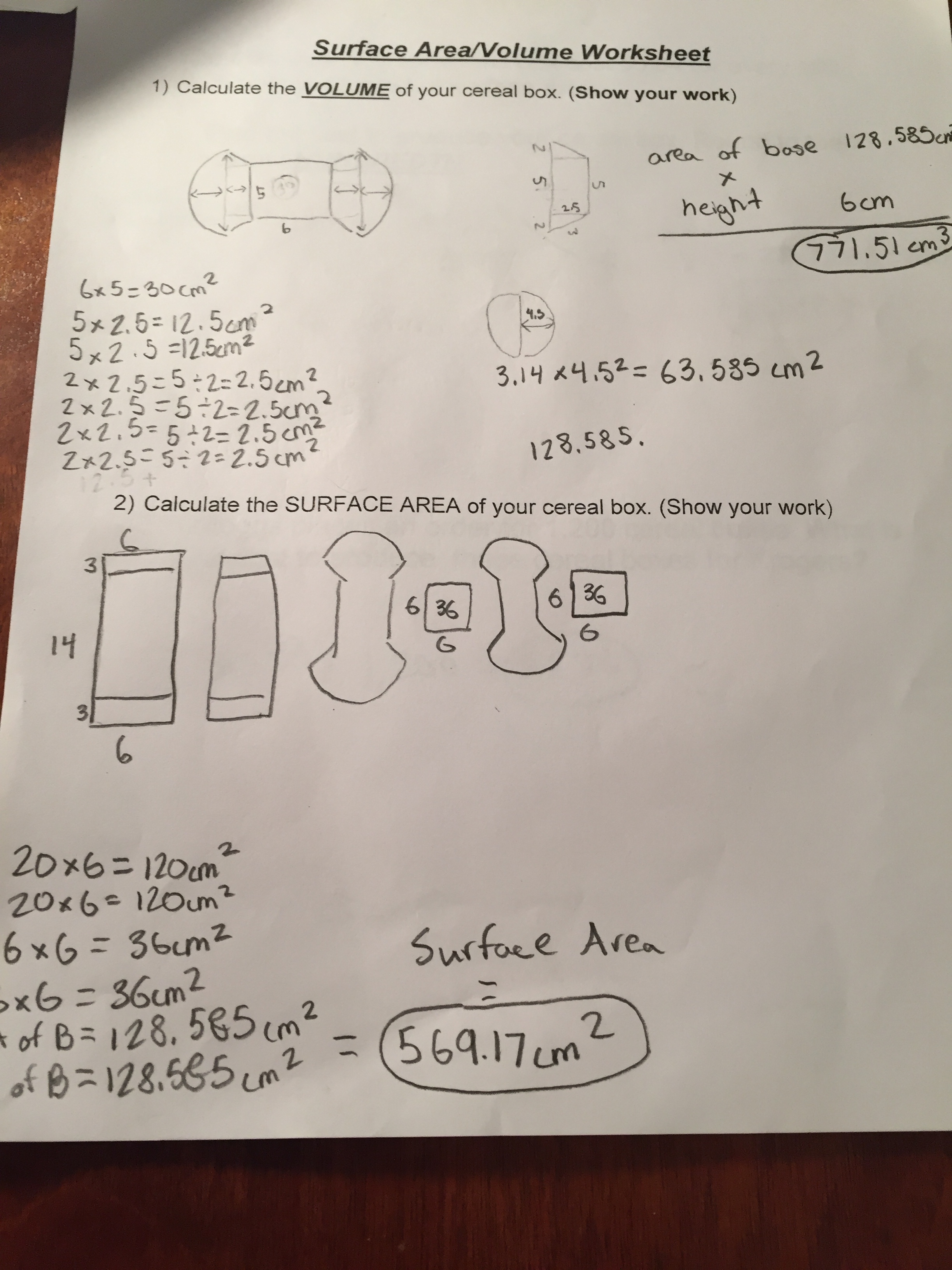
Step 8 - Complete the required paperwork
We usually have students calculate the surface area and volume of their projects. In addition we also have students draw (to scale) Nets and 3D designs of the project.
Lessons Learned from this years Cereal Box Projects
We had another successful year with our cereal box project. Many of the projects were creative and well done. Most of the students were fully engaged in the project. But we did have a couple areas that I need to clean up before next year.
The Curse of the Circle
We had a few students this year build cereal boxes that were either cylinders or had a circle as part of the design. In both of these cases many students just randomly made a circle and just wrapped a long stretch of paper around the circle. There was no thought given to diameter, radius, or circumference. Needless to say, this made for a mess when it came time to make the cereal box the same as its prototype and with calculating surface area and volume.
Struggles with Scissors and Straight lines
Normally I will take a day (or two) to show the students a few tips/tricks when making and cutting out the sides of their project. Because of a time crunch this year, I thought I could save a little time and just give a brief talk and turn them lose. In the end this just created a lot more work for me and made it harder to help out as many students.
Interested in giving the Cereal Box Project a try?
This book will give you an in depth guide to how I use this project in my class.